I am a postdoc at Generative AI group at the Eindhoven University of Technology (TU/e), advised by Jakub M. Tomczak. I did my PhD at AMLab at the University of Amsterdam where I was advised by Jan-Willem van de Meent. I started my PhD at Northeastern University where I was for 4 years before transferring to University of Amsterdam. I got my MSc in Data Science at the University of Edinburgh. I did my BSc in Artificial Intelligence and Computer Science at the same University.
I am interested in deep generative models and how we can guide them towards learning useful representations for downstream tasks. Recently, I also became very interested in making generative models more space efficient via quantization. I am also a big fan of the intersection of information theory and representation learning.
Interests
- Deep Generative Models
- Quantization
- Representation Learning
- Inference
Education
-
PhD in Machine Learning, 2023
University of Amsterdam
-
MSc in Data Science, 2017
University of Edinburgh
-
BSc in Artificial Intelligence and Computer Science, 2016
University of Edinburgh
Featured Publications
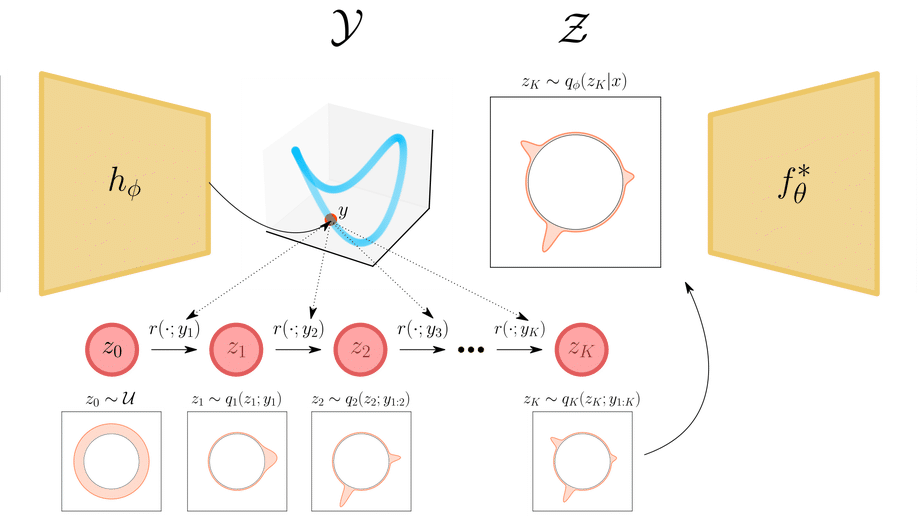
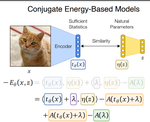
Topological Obstructions and How to Avoid Them
Incorporating geometric inductive biases into models can aid interpretability and generalization, but encoding to a specific geometric structure can be challenging due to the imposed topological constraints. In this paper, we theoretically and empirically characterize obstructions to training encoders with geometric latent spaces. We show that local optima can arise due to singularities (e.g. self-intersection) or due to an incorrect degree or winding number. We then discuss how normalizing flows can potentially circumvent these obstructions by defining multimodal variational distributions. Inspired by this observation, we propose a new flow-based model that maps data points to multimodal distributions over geometric spaces and empirically evaluate our model on 2 domains. We observe improved stability during training and a higher chance of converging to a homeomorphic encoder.
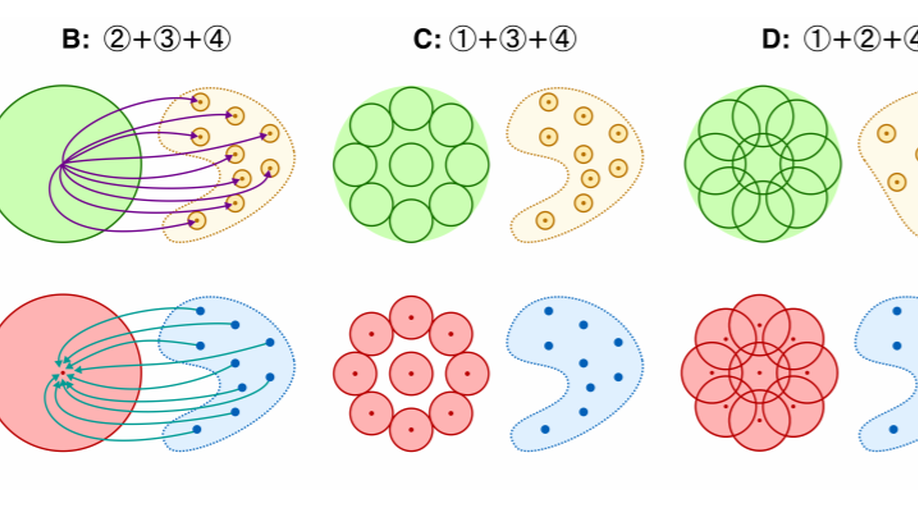
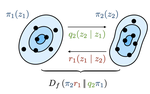
Structured Disentangled Representations
Deep latent-variable models learn representations of high-dimensional data in an unsupervised manner. A number of recent efforts have focused on learning representations that disentangle statistically independent axes of variation by introducing modifications to the standard objective function. These approaches generally assume a simple diagonal Gaussian prior and as a result are not able to reliably disentangle discrete factors of variation. We propose a two-level hierarchical objective to control relative degree of statistical independence between blocks of variables and individual variables within blocks. We derive this objective as a generalization of the evidence lower bound, which allows us to explicitly represent the trade-offs between mutual information between data and representation, KL divergence between representation and prior, and coverage of the support of the empirical data distribution. Experiments on a variety of datasets demonstrate that our objective can not only disentangle discrete variables, but that doing so also improves disentanglement of other variables and, importantly, generalization even to unseen combinations of factors.